Pada
mulanya di zaman purbakala banyak bangsa-bangsa yang bermukim sepanjang
sungai-sungai besar. Bangsa Mesir sepanjang sungai Nil di Afrika,
bangsa Babilonia sepanjang sungai Tigris dan Eufrat, bangsa Hindu
sepanjang sungai Indus dan Gangga, bangsa Cina sepanjang sungai Huang Ho
dan Yang Tze. Bangsa-bangsa itu memerlukan keterampilan untuk
mengendalikan banjir, mengeringkan rawa-rawa, membuat irigasi untuk
mengolah tanah sepanjang sungai menjadi daerah pertanian untuk itu
diperlukan pengetahuan praktis, yaitu pengetahuan teknik dan matematika
bersama-sama.
Sejarah menunjukkan bahwa permulaan Matematika
berasal dari bangsa yang bermukim sepanjang aliran sungai tersebut.
Mereka memerlukan perhitungan, penanggalan yang bisa dipakai sesuai
dengan perubahan musim. Diperlukan alat-alat pengukur untuk mengukur
persil-persil tanah yang dimiliki. Peningkatan peradaban memerlukan cara
menilai kegiatan perdagangan, keuangan dan pemungutan pajak. Untuk
keperluan praktis itu diperlukan bilangan-bilangan.
Awal Bilangan
Bilangan
pada awalnya hanya dipergunakan untuk mengingat jumlah, namun dalam
perkembangannya setelah para pakar matematika menambahkan perbendaharaan
simbol dan kata-kata yang tepat untuk mendefenisikan bilangan maka
matematika menjadi hal yang sangat penting bagi kehidupan dan tak bisa
kita pungkiri bahwa dalam kehidupan keseharian kita akan selalu bertemu
dengan yang namanya bilangan, karena bilangan selalu dibutuhkan baik
dalam teknologi, sains, ekonomi ataupun dalam dunia musik, filosofi dan
hiburan serta banyak aspek kehidupan lainnya.
Bilangan dahulunya
digunakan sebagai symbol untuk menggantikan suatu benda misalnya
kerikil, ranting yang masing-masing suku atau bangsa memiliki cara
tersendiri untuk menggambarkan bilangan dalam bentuk simbol diantaranya :
Simbol bilangan bangsa Babilonia:
Simbol bilangan bangsa Maya di Amerika pada 500 tahun SM:
Simbol bilangan menggunakan huruf Hieroglif yang dibuat bangsa Mesir Kuno:
Simbol bilangan bangsa Arab yang dibuat pada abad ke-11 dan dipakai hingga kini oleh umat Islam di seluruh dunia:
Simbol bilangan bangsa Yunani Kuno:
Simbol bilangan bangsa Romawi yang juga masih dipakai hingga kini:
Dalam
perkembangan selanjutnya, pada abad ke-X ditemukanlah manuskrip Spanyol
yang memuat penulisan simbol bilangan oleh bangsa Hindu-Arab Kuno dan
cara penulisan inilah yang menjadi cikal bakal penulisan simbol bilangan
yang kita pakai hingga saat ini, seperti yang tampak dalam gambar
berikut:
Perkembangan Teori Bilangan
Teori Bilangan Pada suku Babilonia
Matematika
Babilonia merujuk pada seluruh matematika yang dikembangkan oleh bangsa
Mesopotamia (kini Iraq) sejak permulaan Sumeria hingga permulaan
peradaban helenistik. Dinamai “Matematika Babilonia” karena peran utama
kawasan Babilonia sebagai tempat untuk belajar. Pada zaman peradaban
helenistik, Matematika Babilonia berpadu dengan Matematika Yunani dan
Mesir untuk membangkitkan Matematika Yunani. Kemudian di bawah
Kekhalifahan Islam, Mesopotamia, terkhusus Baghdad, sekali lagi menjadi
pusat penting pengkajian Matematika Islam.
Bertentangan dengan
langkanya sumber pada Matematika Mesir, pengetahuan Matematika Babilonia
diturunkan dari lebih daripada 400 lempengan tanah liat yang digali
sejak 1850-an. Lempengan ditulis dalam tulisan paku ketika tanah liat
masih basah, dan dibakar di dalam tungku atau dijemur di bawah terik
matahari. Beberapa di antaranya adalah karya rumahan.
Bukti
terdini matematika tertulis adalah karya bangsa Sumeria, yang membangun
peradaban kuno di Mesopotamia. Mereka mengembangkan sistem rumit
metrologi sejak tahun 3000 SM. Dari kira-kira 2500 SM ke muka, bangsa
Sumeria menuliskan tabel perkalian pada lempengan tanah liat dan
berurusan dengan latihan-latihan geometri dan soal-soal pembagian. Jejak
terdini sistem bilangan Babilonia juga merujuk pada periode ini.
Sebagian
besar lempengan tanah liat yang sudah diketahui berasal dari tahun 1800
sampai 1600 SM, dan meliputi topik-topik pecahan, aljabar, persamaan
kuadrat dan kubik, dan perhitungan bilangan regular, invers perkalian,
dan bilangan prima kembar. Lempengan itu juga meliputi tabel perkalian
dan metode penyelesaian persamaan linear dan persamaan kuadrat.
Lempengan Babilonia 7289 SM memberikan hampiran bagi √2 yang akurat
sampai lima tempat desimal.
Matematika Babilonia ditulis
menggunakan sistem bilangan seksagesimal (basis-60). Dari sinilah
diturunkannya penggunaan bilangan 60 detik untuk semenit, 60 menit untuk
satu jam, dan 360 (60 x 6) derajat untuk satu putaran lingkaran, juga
penggunaan detik dan menit pada busur lingkaran yang melambangkan
pecahan derajat. Juga, tidak seperti orang Mesir, Yunani, dan Romawi,
orang Babilonia memiliki sistem nilai-tempat yang sejati, di mana
angka-angka yang dituliskan di lajur lebih kiri menyatakan nilai yang
lebih besar, seperti di dalam sistem desimal
Teori Bilangan Pada Suku Bangsa Mesir Kuno
Matematika
Mesir merujuk pada matematika yang ditulis di dalam bahasa Mesir. Sejak
peradaban helenistik matematika Mesir melebur dengan matematika Yunani
dan Babilonia yang membangkitkan Matematika helenistik. Pengkajian
matematika di Mesir berlanjut di bawah Khilafah Islam sebagai bagian
dari matematika Islam, ketika bahasa Arab menjadi bahasa tertulis bagi
kaum terpelajar Mesir.
Tulisan matematika Mesir yang paling
panjang adalah Lembaran Rhind (kadang-kadang disebut juga “Lembaran
Ahmes” berdasarkan penulisnya), diperkirakan berasal dari tahun 1650 SM
tetapi mungkin lembaran itu adalah salinan dari dokumen yang lebih tua
dari Kerajaan Tengah yaitu dari tahun 2000-1800 SM. Lembaran itu adalah
manual instruksi bagi pelajar aritmetika dan geometri. Selain memberikan
rumus-rumus luas dan cara-cara perkalian, pembagian, dan pengerjaan
pecahan, lembaran itu juga menjadi bukti bagi pengetahuan matematika
lainnya, termasuk bilangan komposit dan prima; rata-rata aritmetika,
geometri, dan harmonik; dan pemahaman sederhana Saringan Eratosthenes
dan teori bilangan sempurna (yaitu, bilangan 6). Lembaran itu juga
berisi cara menyelesaikan persamaan linear orde satu juga barisan
aritmetika dan geometri.
Naskah matematika Mesir penting lainnya
adalah lembaran Moskwa, juga dari zaman Kerajaan Pertengahan, bertarikh
kira-kira 1890 SM. Naskah ini berisikan soal kata atau soal cerita, yang
barangkali ditujukan sebagai hiburan.
Teori Bilangan Pada Suku Bangsa India
Sulba
Sutras (kira-kira 800–500 SM) merupakan tulisan-tulisan geometri yang
menggunakan bilangan irasional, bilangan prima, aturan tiga dan akar
kubik; menghitung akar kuadrat dari 2 sampai sebagian dari seratus
ribuan; memberikan metode konstruksi lingkaran yang luasnya menghampiri
persegi yang diberikan, menyelesaikan persamaan linear dan kuadrat;
mengembangkan tripel Pythagoras secara aljabar, dan memberikan
pernyataan dan bukti numerik untuk teorema Pythagoras.
Kira-kira
abad ke-5 SM merumuskan aturan-aturan tata bahasa Sanskerta menggunakan
notasi yang sama dengan notasi matematika modern, dan menggunakan
aturan-aturan meta, transformasi, dan rekursi. Pingala (kira-kira abad
ke-3 sampai abad pertama SM) di dalam risalah prosodynya menggunakan
alat yang bersesuaian dengan sistem bilangan biner. Pembahasannya
tentang kombinatorika bersesuaian dengan versi dasar dari teorema
binomial. Karya Pingala juga berisi gagasan dasar tentang bilangan
Fibonacci.
Pada sekitar abad ke 6 SM, kelompok Pythagoras
mengembangkan sifat-sifat bilangan lengkap (perfect number), bilangan
bersekawan (amicable number), bilangan prima (prime number), bilangan
segitiga (triangular number), bilangan bujur sangkar (square number),
bilangan segilima (pentagonal number) serta bilangan-bilangan segibanyak
(figurate numbers) yang lain. Salah satu sifat bilangan segitiga yang
terkenal sampai sekarang disebut triple Pythagoras, yaitu : a.a + b.b =
c.c yang ditemukannya melalui perhitungan luas daerah bujur sangkar yang
sisi-sisinya merupakan sisi-sisi dari segitiga siku-siku dengan sisi
miring (hypotenosa) adalah c, dan sisi yang lain adalah a dan b. Hasil
kajian yang lain yang sangat popular sampai sekarang adalah pembedaan
bilangan prima dan bilangan komposit. Bilangan prima adalah bilangan
bulat positif lebih dari satu yang tidak memiliki Faktor positif kecuali
1 dan bilangan itu sendiri. Bilangan positif selain satu dan selain
bilangan prima disebut bilangan komposit. Catatan sejarah menunjukkan
bahwa masalah tentang bilangan prima telah menarik perhatian
matematikawan selama ribuan tahun, terutama yang berkaitan dengan berapa
banyaknya bilangan prima dan bagaimana rumus yang dapat digunakan untuk
mencari dan membuat daftar bilangan prima.
Dengan berkembangnya
sistem numerasi, berkembang pula cara atau prosedur aritmetis untuk
landasan kerja, terutama untuk menjawab permasalahan umum, melalui
langkah-langkah tertentu, yang jelas yang disebut dengan algoritma. Awal
dari algoritma dikerjakan oleh Euclid. Pada sekitar abad 4 S.M, Euclid
mengembangkan konsep-konsep dasar geometri dan teori bilangan. Buku
Euclid yang ke VII memuat suatu algoritma untuk mencari Faktor
Persekutuan Terbesar dari dua bilangan bulat positif dengan menggunakan
suatu teknik atau prosedur yang efisien, melalui sejumlah langkah yang
terhingga. Kata algoritma berasal dari algorism. Pada zaman Euclid,
istilah ini belum dikenal. Kata Algorism bersumber dari nama seorang
muslim dan penulis buku terkenal pada tahun 825 M., yaitu Abu Ja’far
Muhammed ibn Musa Al-Khowarizmi. Bagian akhir dari namanya
(Al-Khowarizmi), mengilhami lahirnya istilah Algorism. Istilah algoritma
masuk kosakata kebanyakan orang pada saat awal revolusi komputer, yaitu
akhir tahun 1950.
Pada abad ke 3 S.M., perkembangan teori
bilangan ditandai oleh hasil kerja Erathosthenes, yang sekarang terkenal
dengan nama Saringan Erastosthenes (The Sieve of Erastosthenes). Dalam
enam abad berikutnya, Diopanthus menerbitkan buku yang bernama
Arithmetika, yang membahas penyelesaian persamaan didalam bilangan bulat
dan bilangan rasional, dalam bentuk lambang (bukan bentuk/bangun
geometris seperti yang dikembangkan oleh Euclid). Dengan kerja bentuk
lambang ini, Diopanthus disebut sebagai salah satu pendiri aljabar.
Teori Bilangan Pada Masa Sejarah (Masehi)
Awal
kebangkitan teori bilangan modern dipelopori oleh Pierre de Fermat
(1601-1665), Leonhard Euler (1707-1783), J.L Lagrange (1736-1813), A.M.
Legendre (1752-1833), Dirichlet (1805-1859), Dedekind (1831-1916),
Riemann (1826-1866), Giussepe Peano (1858-1932), Poisson (1866-1962),
dan Hadamard (1865-1963). Sebagai seorang pangeran matematika, Gauss
begitu terpesona terhadap keindahan dan kecantikan teori bilangan, dan
untuk melukiskannya, ia menyebut teori bilangan sebagai the queen of
mathematics.
Pada masa ini, teori bilangan tidak hanya berkembang
sebatas konsep, tapi juga banyak diaplikasikan dalam berbagai bidang
ilmu pengetahuan dan teknologi. Hal ini dapat dilihat pada pemanfaatan
konsep bilangan dalam metode kode baris, kriptografi, komputer, dan lain
sebagainya
Tokoh-Tokoh Teori Bilangan
Pythagoras (582-496 SM)
Pythagoras
adalah seorang matematikawan dan filsuf Yunani yang paling dikenal
melalui teoremanya. Dikenal sebagai “Bapak Bilangan”, dia memberikan
sumbangan yang penting terhadap filsafat dan ajaran keagamaan pada akhir
abad ke-6 SM.
Salah satu peninggalan Pythagoras yang terkenal
adalah teorema Pythagoras, yang menyatakan bahwa kuadrat hipotenusa dari
suatu segitiga siku-siku adalah sama dengan jumlah kuadrat dari
kaki-kakinya (sisi-sisi siku-sikunya). Walaupun fakta di dalam teorema
ini telah banyak diketahui sebelum lahirnya Pythagoras, namun teorema
ini dikreditkan kepada Pythagoras karena ia yang pertama kali
membuktikan pengamatan ini secara matematis.
Jamshid Al-Kashi (1380 M)
Al-Kashi
terlahir pada 1380 di Kashan, sebuah padang pasir di sebelah utara
wilayah Iran Tengah. Selama hidupnya, al-Kashi telah menyumbangkan dan
mewariskan sederet penemuan penting bagi astronomi dan matematika.
Pecahan
desimal yang digunakan oleh orang-orang Cina pada zaman kuno selama
berabad-abad, sebenarnya merupakan pecahan desimal yang diciptakan oleh
al-Kashi. Pecahan desimal ini merupakan salah satu karya besarnya yang
memudahkan untuk menghitung aritmatika yang dia bahas dalam karyanya
yang berjudul Kunci Aritmatika yang diterbitkan pada awal abad ke-15 di
Samarkand.
Abu Ali Hasan Ibnu Al-Haytam (965 M)
Abu
Ali Hasan Ibnu Al-Haytam lahir Basrah Irak, yang oleh masyarakat Barat
dikenal dengan nama Alhazen. Al-Haytam adalah orang pertama yang
mengklasifikasikan semua bilangan sempurna yang genap, yaitu bilangan
yang merupakan jumlah dari pembagi-pembagi sejatinya, seperti yang
berbentuk 2k-1(2k-1) di mana 2k-1 adalah bilangan prima. Selanjutnya
Al-Haytam membuktikan bahwa bila p adalah bilangan prima, 1+(p-1)! habis
dibagi oleh p.
Pierre de Fermat
Fermat
menuliskan bahwa “I have discovered a truly remarkable proof which this
margin is to small to contain”. Fermat juga hampir selalu menulis
catatan kecil sejak tahun 1603, manakala ia pertama kali mempelajari
Arithmetica karya Diophantus. Ada kemungkinan Fermat menyadari bahwa apa
yang ia sebut sebagai remarkable proof ternyata salah, karena semua
teorema yang dia nyatakan biasanya dalam bentuk tantangan yang Fermat
ajukan terhadap matematikawan lain. Meskipun kasus khusus untuk n = 3
dan n = 4 ia ajukan sebagai tantangan (dan Fermat mengetahui bukti untuk
kasus ini) namun teorema umumnya tidak pernah ia sebut lagi. Pada
kenyataannya karya matematika yang ditinggalkan oleh Fermat hanya satu
buah pembuktian. Fermat membuktikan bahwa luas daerah segitiga siku-
siku dengan sisi bilangan bulat tidak pernah merupakan bilangan kuadrat.
Jelas hal ini mengatakan bahwa tidak ada segitiga siku-siku dengan sisi
rasional yang mempunyai luas yang sama dengan suatu bujursangkar dengan
sisi rasional. Dalam simbol, tidak terdapat bilangan bulat x, y, z
dengan sehingga bilangan kuadrat. Dari sini mudah untuk mendeduksi kasus
n = 4, Teorema Fermat. Penting untuk diamati bahwa dalam tahap ini yang
tersisa dari pembuktian Fermat Last Theorem adalah membuktikan untuk
kasus n bilangan prima ganjil. Jika terdapat bilangan bulat x, y, z
dengan maka jika n = pq, .
Kapankah angka nol ditemukan?
Zero
= 0 = Empty = Kosong (Nol) Memang, kata dalam Bahasa Inggris ‘zero’
(nol) berasal dari bahasa Arab ‘sifr’, suatu terjemahan literal dari
bahasa Sanskrit “shûnya” yang bermakna “kosong”. Runtutan keterkaitan
bahasa dari masa ke masa: shûnya (Sanskrit) -> (Ancient
Egypt/Babylonia) -> (Greek/Helenic) -> (Rome/Byzantium) – sifr
(Arab) -> zero (English) -> nol; kosong (Indonesia) Wikipedia The
word “zero” comes ultimately from the Arabic “sifr”, or “empty,” a
literal translation of the Sanskrit “shûnya”. With its new use for the
concept of zero, zephyr came to mean a light breeze – “an almost
nothing” (Ifrah 2000; see References). The word zephyr survives with
this meaning in English today. The Italian mathematician Fibonacci
(c.1170-1250), who grew up in Arab North Africa and is credited with
introducing the Arabic decimal system to Europe. Around the same time,
the Arab mathematician al-Khwarizmi described the “Hindu number” system
with positional notation and a zero symbol in his book Kitab al-jabr
wa’l muqabalah. Nol asalnya dari India “shûnya” bukan cuma sebuah
istilah, tapi juga konsep.
Sekitar tahun 300 SM orang babilonia
telah memulai penggunaan dua buah baji miring, //, untuk menunjukkan
sebuah tempat kosong, sebuah kolom kosong pada Abakus. Simbol ini
memudahkan seseorang untuk menentukan letak sebuah symbol. Angka nol
sangat berguna dan merupakan simbol yang menggambarkan sebuah tempat
kosong dalam Abakus, sebuah kolom dengan batu-batu yang ditempatkan di
dasar. Kegunaannya hanya untuk memastikan bahwa butiran-butiran tersebut
berada di tempat yang tepat, angka nol tidak memiliki nilai numeric
tersendiri.
Pada komputer nol ini dapat merusak sistem, karena nol
diartikan tidak ada. Berapapun bilangan dikalikan dengan nol hasilnya
tidak ada. Nah inilah yang membuat bingung dalam operasi perhitungan.
Perhatikan contoh ini :
0=0 ( nol sama dengan nol, benar)
0 x3=0 x 89 (nol sama-sama dikalikan dengan sebuah bilangan, karena juga akan bernilai nol)
(0 x 3)/0= (0 x 89)/0 (sebuah bilangan dibagi dengan bilangan yang sama, akan bernilai satu)
3=89 (???, hasil ini yang membuat bingung)
Walaupun
demikian sebenarnya nol itu hebat, jika tidak ditemukan angka nol
tulisan satu juta dalam bilangan romawi ditulis apa?? Bisa-bisa selembar
kertas tidak sampai untuk hanya memberikan symbol satu juta itu. Bisa
dibayangkan jika nol tidak ada. Banyak kekuatan yang terkandung dalam
angka ini. Nol adalah perangkat paling penting dalam matematika. Namun
berkat sifat matematis dan filosofis yang aneh pada angka nol, ia akan
berbenturan dengan filsafat barat.
Angka nol berbenturan dengan
salah satu prinsip utama filsafat barat, sebuah dictum yang akar-akarnya
terhujam dalam filsafat angka Phythagoras dan nilai pentingnya tumbuh
dari paradoks Zeno. seluruh cosmos Yunani didirikan di atas pilar: tak
ada kekosongan.
Kosmos Yunani yang dis=ciptakan oleh Phytagoras,
Aristoteles dan Ptolemeus masih lama bertahan setelah keruntuhan
peradaban Yunani. Dalam kosmos ini tak ada ketiadaaan. Oleh karena itu,
hampir sepanjang dua milinium orang-orang barat tak bersedia menerima
angka nol. Konsekuensinya sungguh menakutkan. Ketiadaan angka nol
menghambat perkembangan matematika, menghalangi inovasi sains dan yang
lebih berbahaya, mengacaukan sistem penanggalan.
Macam-macam bilangan
Bilangan Bulat adalah bilangan yang terdiri atas bilangan positif, bilangan nol, dan bilangan negatif.
Misal : ….-2,-1,0,1,2….
Bilangan asli adalah bilangan bulat positif yang diawali dari angka 1(satu) sampai tak terhingga.
Misal : 1,2,3….
Bilangan cacah adalah bilangan bulat positif yang diawali dari angka 0 (nol) sampai tak terhingga.
Misal : 0,1,2,3,….
Bilangan prima adalah bilangan yang tepat mempunyai dua faktor yaitu bilangan 1 (satu) dan bilangan itu sendiri.
Misal : 2,3,5,7,11,13,…..
(1 bukan bilangan prima, karena mempunyai satu faktor saja).
Bilangan komposit adalah bilangan yang bukan 0, bukan 1 dan bukan bilangan prima.
Misal ; 4,6,8,9,10,12,….
Bilangan
rasional adalah bilangan yang dinyatakan sebagai suatu pembagian antara
dua bilangan bulat (berbentuk bilangan a/b, dimana a dan b merupakan
bilangan bulat).
Misal: 1/2 ,2/(3 ),3/4….
Bilangan irrasional adalah bilangan yang tidak dapat dinyatakan sebagai pembagian dua bilangan bulat.
Misal: π, √3 , log 7 dan sebagainya.
Bilangan riil adalah bilangan yang merupakan penggabungan dari bilangan rasional dan bilangan irrasional
Misal: 1/2 √(2 ),1/3 √5,1/4 π,2/3 log2 dan sebagainya.
Bilangan
imajiner (bilangan khayal) adalah bilangan yang ditandai dengan i,
bilangan imajiner i dinyatakan sebagai √(-1). Jadi, jika i = √(-1) maka
i2= -1
Misal: √(-4)=⋯?
√(-4)=√(4×(-1) )
= √4×√(-1)
= 2 × i
= 2i
Jadi, √(-4)=2i.
Bilangan kompleks adalah bilangan yang merupakan penggabungan dari bilangan riil dan bilangan imajiner.
Misal; π√(-1)= πi
Log √(-1)=logi
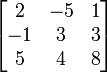 ditranspose menjadi AT =
ditranspose menjadi AT = 
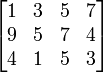 ditranspose menjadi BT =
ditranspose menjadi BT = 

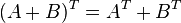 dan
dan 
 dimana k adalah skalar
dimana k adalah skalar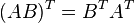
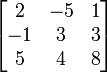 ditranspose menjadi AT =
ditranspose menjadi AT = 
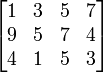 ditranspose menjadi BT =
ditranspose menjadi BT = 

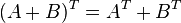 dan
dan 
 dimana k adalah skalar
dimana k adalah skalar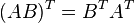
 Ide-ide ini adalah sistematis ke dalam kalkulus sejati infinitesimals oleh Gottfried Wilhelm Leibniz, yang pada awalnya dituduh plagiarisme
oleh Newton. Dia sekarang dianggap sebagai penemu independen dan
kontributor kalkulus. Nya kontribusi adalah untuk menyediakan sebuah set
aturan untuk memanipulasi jumlah yang sangat kecil, memungkinkan
perhitungan turunan kedua dan lebih tinggi, dan menyediakan aturan produk dan aturan rantai,
dalam diferensial dan bentuk integral. Tidak seperti Newton, Leibniz
membayar banyak perhatian pada formalisme, sering menghabiskan hari-hari
menentukan simbol-simbol yang sesuai untuk konsep.
Ide-ide ini adalah sistematis ke dalam kalkulus sejati infinitesimals oleh Gottfried Wilhelm Leibniz, yang pada awalnya dituduh plagiarisme
oleh Newton. Dia sekarang dianggap sebagai penemu independen dan
kontributor kalkulus. Nya kontribusi adalah untuk menyediakan sebuah set
aturan untuk memanipulasi jumlah yang sangat kecil, memungkinkan
perhitungan turunan kedua dan lebih tinggi, dan menyediakan aturan produk dan aturan rantai,
dalam diferensial dan bentuk integral. Tidak seperti Newton, Leibniz
membayar banyak perhatian pada formalisme, sering menghabiskan hari-hari
menentukan simbol-simbol yang sesuai untuk konsep.